Мова рухів

Якщо ви знайомі з мовою рухів для кубика Рубіка, то мова рухів для пірамінкса не стане для вас проблемою. Кожна з чотирьох вершин пірамінкса має свою назву, як показано на малюнку справа. Рухи одного шару, тобто рухи маленьких вершинок не використовуються у алгоритмах. Але у перемішувальних алгоритмах можна побачити маленькі рухи r, l, b, u – що означають саме рухи цих вершинок. Відповідно, рухи двох шарів будуть позначатись як R, L, B, U.
Іноді можна зустріти подвійні рухи R2, L2, B2, U2, які по суті не відрізняються від рухів проти чи за годинниковою стрілкою, але іноді це робиться для позначення більш зручного виконання алгоритмів (наприклад, R L R2′ L’ R).

Кожна грань пірамінкса має 3 центральні наклейки, які своїм малюнком нагадують символ радиації. Умовно, це можна назвати хрестом для пірамінкса.
Загалом пірамінкс має 4 центральні елементи, 6 ребер і 4 вершинки.

1. Центри, вершинки і 2 ребра

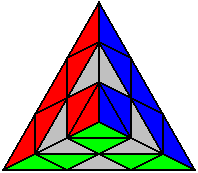
На зображенні зліва можна побачити, як саме має виглядати пірамінкс після першого етапу. Необхідно правильно орієнтувати всі центральні елементи разом з вершинками, і вирішити два ребра. Це здається повноцінним першим етапом, але насправді це дуже легко.

Перемішана пірамідка дозволяє в першу чергу правильно поставити центри і вирівняти вершинки. Для того щоб визначити, на якій стороні який колір збирати, погляньте на будь-яку вершинку. Колір, якого на ній нема, і буде кольором протилежної грані.

Після цього необхідно знайти два будь-яких ребра, що мають стояти поруч і простими рухами (R U R’ U’), (R U’ R’ U), (R’ U R U’), чи (R’ U’ R U) поставити їх на місце. Вірне положення ребра визначається за кольорами суміжних центрів.

Трохи тренувань, і ви зможете за 15 секунд огляду прорахувати центри і одне, чи навіть два ребра. Наприклад, якщо ви відразу бачите ребро, що прикріплено до свого центру, то саме з цієї сторони і необхідно збирати інші два центри та друге ребро.

2. Останні 4 ребра (Last 4 edges)

Єдине що залишилось – це зібрати останні 4 ребра. Тримайте головоломку так, щоб третє ребро, яке необхідне для розв’зання нижнього шару було між нижньою та передньою гранню.
Усього випадків для такого положення – 96, з яких один – розв’язаний стан. Вам необхідно вивчити усі ці алгоритми, якщо ви хочете виконувати цей етап за один раз.

Випадки відсортовані по групах, в залежності від розташування нижнього нерозв’язаного ребра. На малюнках це зелено-жовте ребро. Якщо ви хочете досягнути максимального успіху, вам необхідно бути нейтральним до кольорів, і вміти розпізнавати випадки незалежно від того, з якої сторони ви починали розв’язок.

Математика

Не враховуючи прості алгоритми першого етапу, цей метод налічує 95 алгоритмів. Якщо ви захочете спочатку розв’язувати нижнє ребро, а потім верхній шар, то вам необхідно буде вивчити лише 11 алгоритмів, з яких половина – зеркальні.
Враховуючи як рухи двох шарів, так і орієнтування вершинок, для розв’язку першого етапу необхідно в середньому 41/3 ≈ 13.67 рухів. Якщо повноцінно виконувати другий етап, то для нього в середньому необхідно 161/24 ≈ 6.71 рухів. Загальна кількість рухів для розв’язку у такий спосіб – 163/8 ≈ 20.38 рухів.
Якщо використовувати look ahead, то перед другим етапом іноді можна побачити недовернутий випадок, і зекономити рух U чи U’. Отже середня кількість рухів при ідеальному використанні цього методу може складати 315/16 ≈ 19.69 рухів. Звісно че число можна суттєво зменшити, якщо ефективно прорахувати перший етап.

Група 1

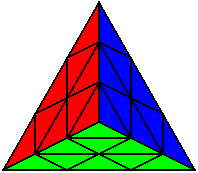Розв’язано!
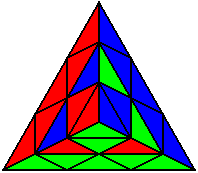R U’ R’ U’ R U’ R’
R’ U’ R U’ R’ U’ R
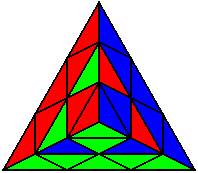R U R’ U R U’ R’
R’ U R U R’ U R
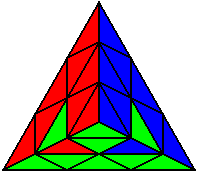U L U’ R U’ R’ U L’
L U’ R U R’ U L’ U’
R’ L R L’ U L’ U’ L
L R’ L’ R U’ R U R’

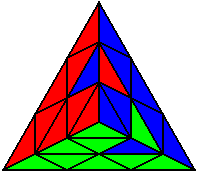R’ U L’ U L U’ R U’
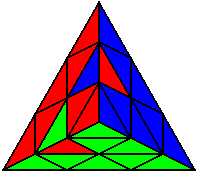L U’ R U’ R’ U L’ U
L U R U’ R’ L’
L’ B’ U’ B U L
R’ L’ U’ L U R
R U B U’ B’ R’

B’ R’ U’ R U B
B U L U’ L’ B’
L R U R’ U’ L’
L’ U’ B’ U B L
R’ U’ L’ U L R
R B U B’ U’ R’
B’ U’ R’ U R B
B L U L’ U’ B’

Група 2

R L’ U L U’ L R’ L’
R U’ R’ U L’ U L U’
U’ R U’ R’ U L’ U L
U L’ U L U’ R U’ R’
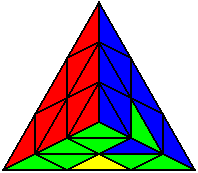L’ R U’ R’ U R’ L R
L’ U L U’ R U’ R’ U
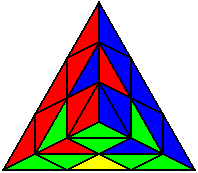U L’ U L R U’ B U’ B’ R’
R B U B’ U R’ L’ U’ L U’

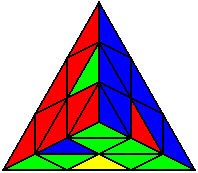U’ L’ B’ U B’ L’ B’ L’
U’ R’ B’ R’ B’ U B’ R’
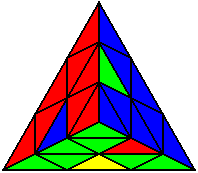U L B L B U’ B L
U R B U’ B R B R
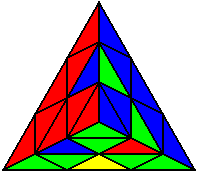R U’ R’ L’ U’ L U’
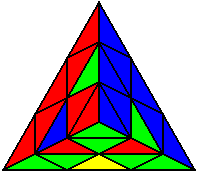U’ R U’ R’ L’ U’ L

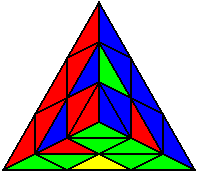U R U’ R’ L’ U’ L U
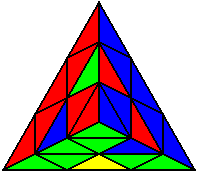U’ L’ U L R U R’ U’
U L’ U L R U R’
L’ U L R U R’ U

Група 3

U’ L’ B’ U B L
L R’ B L B’ L R
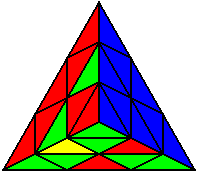U R’ L R L U’ L
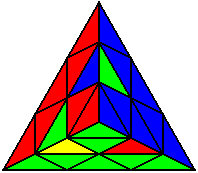U L R L U’ L’ R’ L’

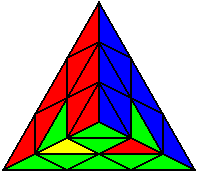U L’ U’ L
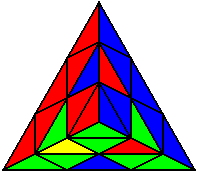R U R’ U L’ U L
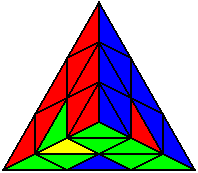L R’ L’ R
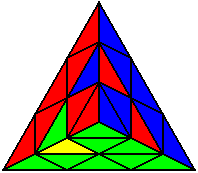U L’ B’ U’ B U’ L U

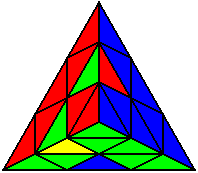U’ L’ U L
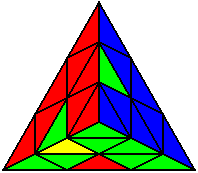L’ B L’ B’ L’
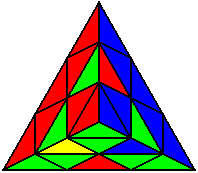U R U’ R’ U L’ U’ L
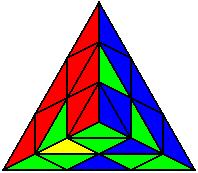U L’ U B’ U B L

Група 4

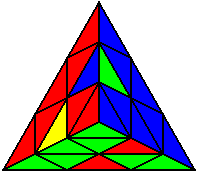L’ U L R U’ R’
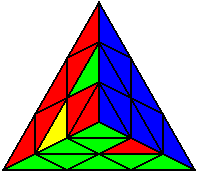U’ R U B’ R B R
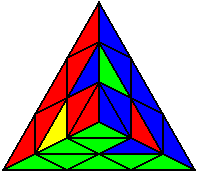U’ R U R’ U R U’ R’
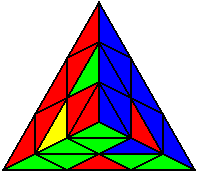L R L U L’ R’ L’ U’

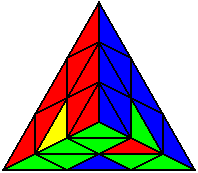R U’ R’ U
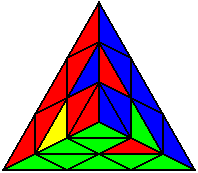U L’ U L U’ R U R’ U
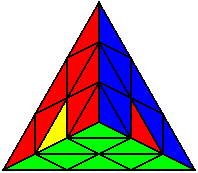U L B L B’ L U’
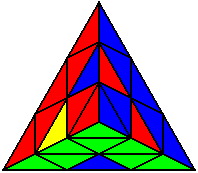U R U’ B U’ B’ R’ U

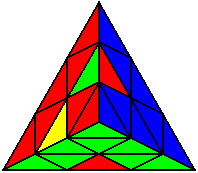U R U R’ U
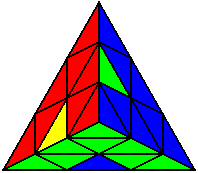U’ R’ L R L’ U
R’ B’ R’ B’ U’ B’ R’ U
U R B U B’ U R’

Група 5

U’ R U R’
R’ L R L’
L’ U’ L U’ R U’ R’
U’ R B U B’ U R’ U’

U R B U’ B’ R’
U’ L R’ L’ R’ U R’
R’ L B’ R’ B R’ L’
U’ R’ L’ R’ U R L R

U R U’ R’
U’ L’ U L U’ R U R’
R B’ R B R
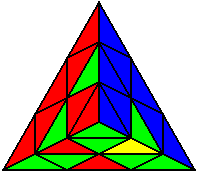U’ R U’ B U’ B’ R’

Група 6

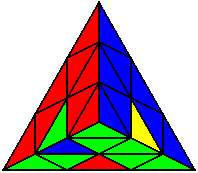L’ U L U’
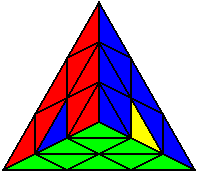U’ R’ B’ R’ B R’ U
U’ R U’ R’ U L’ U’ L U’
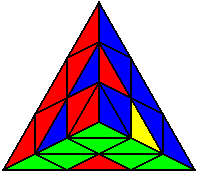U’ L’ U B’ U B L U’

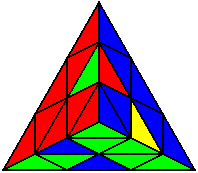R U’ R’ L’ U L
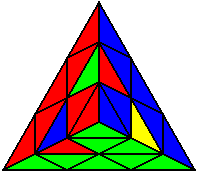U L’ U’ L U’ L’ U L
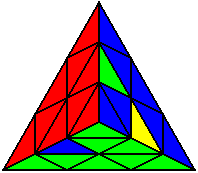U L’ U’ B L’ B’ L’
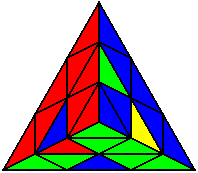R’ L’ R’ U’ R L R U

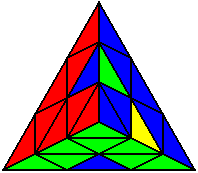U’ L’ U’ L U’
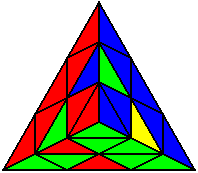L B L B U B L U’
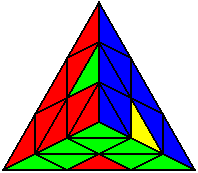U L R’ L’ R U’
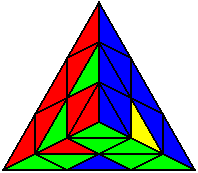U’ L’ B’ U’ B U’ L

Група 7

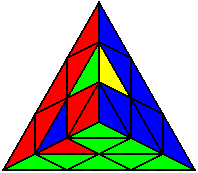U’ R U’ R’ U’
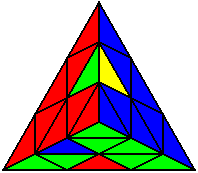L B L B’ L
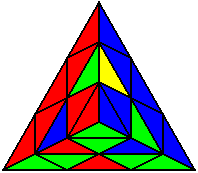L R B’ R L B L R
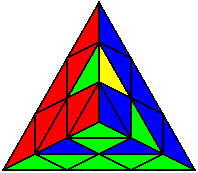R U’ B U’ B’ R’ U’

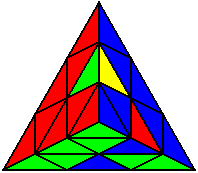R U R’ U’
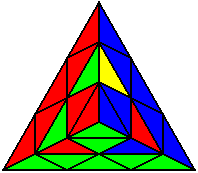U L’ B’ U’ B’ L’ B’ L’
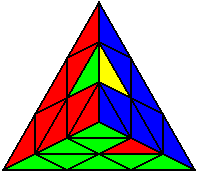U R’ L R L’ U’
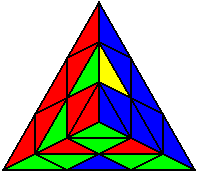R B U B’ U R’ U

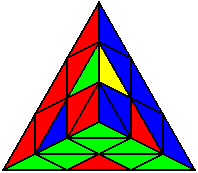U R U’ R L R L’
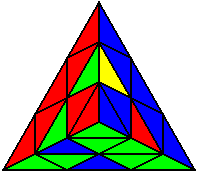U’ L R L U L’ R’ L’
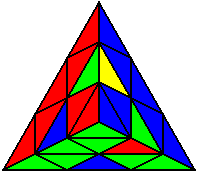U’ L’ B’ U’ B L U’
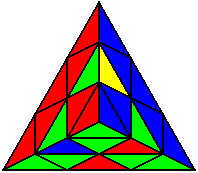U R U’ R’ U’ R U R’

Група 8

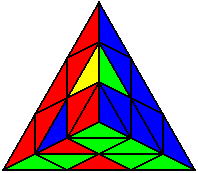L’ U’ L U
U’ L R’ L’ R U
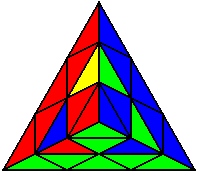U’ R B U B R B R
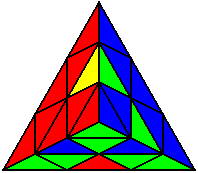L’ B’ U’ B U’ L U’

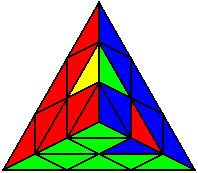U L’ U L U
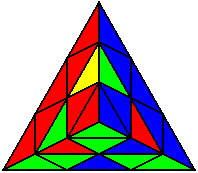R’ L’ B L’ R’ B’ R’ L’
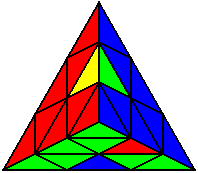R’ B’ R’ B R’
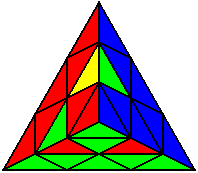L’ U B’ U B L U

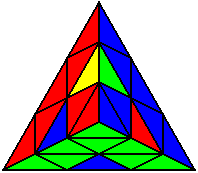U’ L’ U L’ R’ L’ R
U R B U B’ R’ U
U R’ L’ R’ U’ R L R
U’ L’ U L U L’ U’ L